ഗണിതം സുന്ദരം : Deepika.com Special News

ഗണിതം സുന്ദരം

പരീക്ഷയെന്നാൽ പരീക്ഷണം തന്നെ. അതിനെ സധൈര്യം നേരിടാൻ തയാറെടുപ്പു വേണം. ചോദ്യമാതൃകകൾ അറിയണം.ഉത്തരങ്ങൾ മനസ്സിലാക്കണം.പ്രധാനപ്പെട്ട സൂത്രവാക്യങ്ങളും സൂചകങ്ങളും മനഃപാഠമാക്കണം.പഠിച്ച കാര്യങ്ങളെ ആശയങ്ങളെ,സങ്കല്പങ്ങളെ വ്യത്യസ്തങ്ങളായ സന്ദർത്തിൽ പ്രയോഗിക്കാനുള്ള കഴിവുണ്ടാകണം.എല്ലാ കുഞ്ഞുകൂട്ടുകാർക്കും വിജയാശംസകൾ.

1.സമാന്തരശ്രേണികൾ

പ്രധാന ആശയങ്ങൾ

1. ഏതു സമാന്തരശ്രേണിയുടെയും ബീജഗണിതരൂപം Xn= an+b ‘a’ എന്നത് പൊതുവ്യത്യാസവും a+b എന്നത് ആദ്യപദവും ആണ്.
2. ഒന്നാം പദം തന്നാൽ,പത്താം പദം X10=f+9d
നാലാം പദം തന്നാൽ,പത്താം പദം X10=f+6d
3. ഒന്നാം പദം f പൊതുവ്യത്യാസം d എങ്കിൽ n-ാംപദം =f+(n+1)d.
4. n-ാം പദത്തിനെ ശ്രേണിയുടെ ബീജഗണിതരൂപം എന്നും പറയും
5. ഏതെങ്കിലും രണ്ട് പദങ്ങൾ Xm , Xn തന്നാൽ പൊതുവ്യത്യാസം

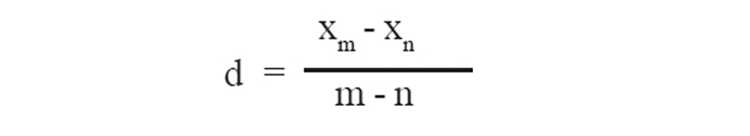
6. a,b,c എന്നിവ ഒരു ശ്രേണിയുടെ തുടർച്ചയായ 3 പദങ്ങൾ ആണെങ്കിൽ മധ്യപദം

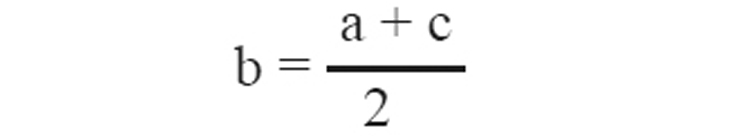
7. ഒരു സമാന്തരശ്രേണിയുടെ ഏത് രണ്ട് പദങ്ങളുടെ വ്യത്യാസവും പൊതുവ്യത്യാസത്തിന്‍റെ ഗുണിതമായിരിക്കും.
8. ഒരു സമാന്തരശ്രേണിയുടെ ഏതൊരു പദത്തിനെയും പൊതുവ്യത്യാസം കൊണ്ട് ഹരിച്ചാൽ ഒരേ ശിഷ്ടം ലഭിക്കും.
9. ഒന്നു മുതൽ തുടർച്ചയായ n എണ്ണൽ സംഖ്യകളുടെ തുക 1+2+3+......+n=

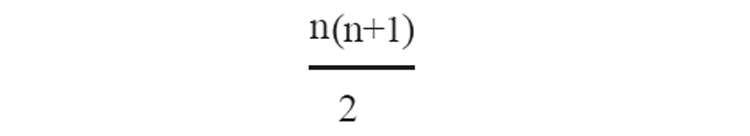
10. സമാന്തരശ്രേണിയിലെ പദങ്ങളുടെ തുക =

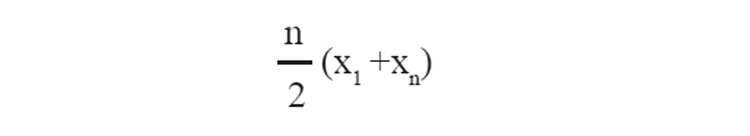
11. സമാന്തരശ്രേണിയിലെ പദങ്ങളുടെ തുക =

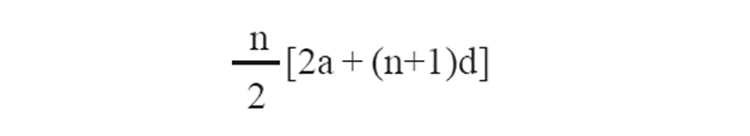
12. ആദ്യപദം X1,അവസാനപദം Xn, പൊതുവ്യത്യാസം xd എങ്കിൽ പദങ്ങളുടെ എണ്ണം

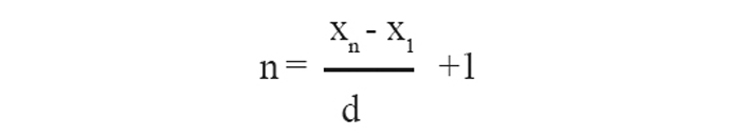
13. ഒരു സമാന്തരശ്രേണിയുടെ രണ്ട് അറ്റങ്ങളിൽ നിന്നും തുല്യ സ്ഥാനത്തുള്ള പദജോഡികളുടെ തുകകൾ തുല്യമായിരിക്കും.ഉദാഹരണത്തിന് സമാന്തരശ്രേണിയുടെ പദങ്ങളാണ് X1, X2, X3, X4, X5, X6, X7, X8, X9, X10 എങ്കിൽ X1+X10= X2+X9= X3+X8= X4+X7= X5+X6 ആയിരിക്കും.
14. ഒരു സമാന്തരശ്രേണിയുടെ തുകയുടെ Aബീജഗണിതരൂപം എപ്പോഴും an2 +bn എന്നായിരിക്കും.അതിന്‍റെ പൊതുവ്യത്യാസം n2 ഗുണകത്തിന്‍റെ ഇരട്ടി 2a ആയിരിക്കും.ഒന്നാം പദം ഗുണകങ്ങളുടെ തുക a+b ആയിരിക്കും.

ചോദ്യങ്ങൾ

1. (n+2)2- ( n-2)2 എന്ന ബീജഗണിതവാചകത്തിൽ n-ന് 1 മുതൽ തുടർച്ചയായ എണ്ണൽ സംഖ്യാവിലകൾ നൽകിയാൽ കിട്ടുന്ന സംഖ്യശ്രേണി എഴുതുക.ഈ സംഖ്യശ്രേണിയിൽ 144 എത്രാം പദമാണ്.?
n= 1,2,3,........... കിട്ടുന്നശ്രേണി :8,16,42,31....................
=18

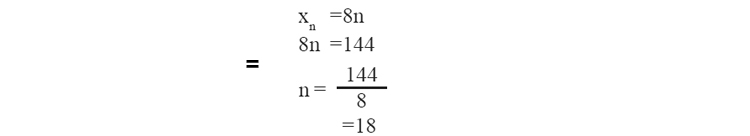
2. 184,178,172,166 ...... എന്ന സമാന്തരശ്രേണിയുടെ
a) ബീജഗണിതരൂപം n-ാം പദം എഴുതുക
b) ഈ ശ്രേണിയിൽ എത്ര അധിസംഖ്യാപദങ്ങൾ ഉണ്ട്?
c) ഈ ശ്രേണിയിലെ ഏറ്റവും വലിയ ന്യൂനസംഖ്യാപദം ഏത്?

ഉത്തരം

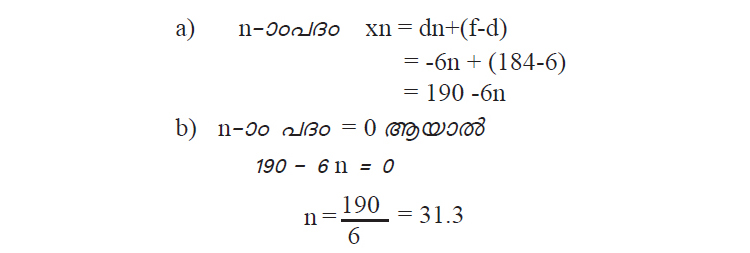
ശ്രേണിയിൽ 31 അധിസംഖ്യാ പദങ്ങൾ ഉണ്ട്.
c) ഏറ്റവും വലിയ ന്യൂനസംഖ്യാപദം
= x 32
= 190 - 6 x 32
= -2
3. ഒരു സമാന്തരശ്രേണിയുടെ m-ാംപദം nഉം n -ാം പാദം ഉം mഉം ആണ്.
a) ശ്രേണിയുടെ പൊതുവ്യത്യാസം എത്ര?
b) ശ്രേണിയുടെ (m+n+p) പദം -p ആണെന്ന് സമർഥിക്കുക.

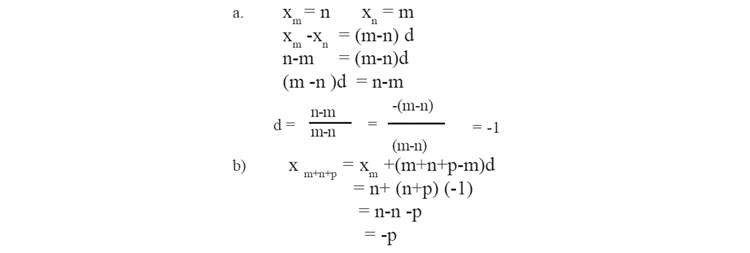
2 & 7 വൃത്തങ്ങളും തൊടുവരകളും

1. ഒരു അർദ്ധവൃത്തത്തിലെ കോണ്‍ 900 ആയിരിക്കും.
2. ഒരു ചാപത്തിലെ കോണുകൾക്കെല്ലാം തുല്യ അളവായിരിക്കും.
3.ഒരു ചാപത്തിന്‍റെ കേന്ദ്രകോണിന്‍റെ പകുതിയായിരിക്കും മറുചാപത്തിലെ കോണ്‍
4. ഒരു ചക്രിയചതുർഭുജത്തിലെ എതിർകോണുകളുടെ തുക 1800 ആയിരിക്കും
5. ഒരു ചാപത്തിന്‍റെയും മറുചാപത്തിന്‍റെയും കേന്ദ്രകോണുകളുടെ തുക 1800 ആയിരിക്കും.
6. ഒരു വൃത്തത്തിലെ ഒരു ബിന്ദുവിൽ വരച്ച തൊടുവര ആ ബിന്ദുവിലേക്കുള്ള ആരത്തിന് ലംബമായിരിക്കും.
7.പുറമെയുള്ള ഒരു ബിന്ദുവിൽ നിന്ന് വൃത്തത്തിലേക്ക് വരക്കുന്ന രണ്ട് തൊടുവരകൾക്കും ഒരേ നീളമായിരിക്കും.
8. പുറമെയുള്ള ഒരു ബിന്ദുവിൽ നിന്ന് വൃത്തത്തിലേക്ക് വരയ്ക്കുന്ന രണ്ട് തൊടു വരകൾക്ക് ഇടയിലുള്ള കോണും,അവയിലേക്കുള്ള ആരങ്ങൾക്കിടയിലുള്ള കോണും കൂട്ടിയാൽ 1800 കിട്ടും.
9. ഒരു വൃത്തത്തിലെ ഒരു ഞാണിന്‍റെ അറ്റത്തു വരയ്ക്കുന്ന തൊടുവര ഞാണുമായി ഒരു ഭാഗത്ത് ഉണ്ടാകുന്ന കോണ്‍ ഞാണിന്‍റെ മറുഭാഗത്തെ വൃത്തഖണ്ഡത്തിലെ കോണിന് തുല്യമായിരിക്കും.
10. വിസ്തീർണ്ണം A യും ചുറ്റളവിന്‍റെ പകുതി S ഉം ആയിട്ടുള്ള ത്രികോണത്തിന്‍റെ അന്തർവൃത്ത
ആരം

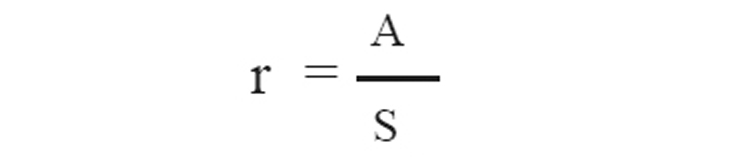
11. വശങ്ങളുടെ a,b,c ഉള്ള ത്രികോണ വിസ്തീർണം

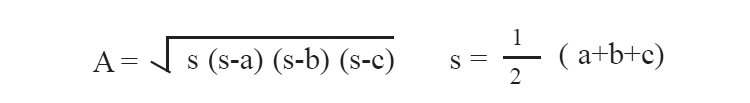
ചോദ്യങ്ങൾ

1. 5 സെന്‍റീമീറ്റർ,6 സെന്‍റീമീറ്റർ, 7 സെന്‍റീമീറ്റർ വശങ്ങളുള്ള ഒരു ത്രികോണം വരയ്ക്കുക. ഈ ത്രികോണത്തിന്‍റെ അന്തർവൃത്തം വരയ്ക്കുക. ഏതെങ്കിലും രണ്ട് കോണുകൾക്ക് സമഭാജി വരയ്ക്കുക. സമഭാജികൾ സംഗമിക്കുന്ന ബിന്ദു കേന്ദ്രമാക്കി കേന്ദ്രത്തിൽ നിന്നും ഒരു വശത്തേക്കുള്ള അകലം ആരമാക്കി വൃത്തം വരയ്ക്കുക.
2. ത്രികോണം ABC യുടെ അളവുകൾ AB = 6സെന്‍റീമീറ്റർ, 3. ആരം 2.5 സെന്‍റീമീറ്റർ ആയ ഒരു വൃത്തം വരയ്ക്കുക. വശങ്ങളെല്ലാം ഈ വൃത്തത്തെ തൊടുന്നതും കോണുകൾ 400,600,800 ആയ ത്രികോണം വരയ്ക്കുക.
4. 3 സെന്‍റീമീറ്റർ ആരമുള്ള ഒരു വൃത്തം വരച്ച് അതിന്‍റെ കേന്ദ്രത്തിൽ നിന്നും 7 സെന്‍റീമീറ്റർ അകലത്തിൽ ഒരു ബിന്ദു അടയാളപ്പെടുത്തുക. ഈ ബിന്ദുവിൽ നിന്ന് വൃത്തത്തിലേക്ക് തൊടുവരകൾ വരയ്ക്കുക.
5. 7 cm നീളവും 5 cm വീതിയുമുള്ള ചതുരം വരച്ച് തുല്യപരപ്പളവുള്ള സമചതുരം നിർമ്മിക്കുക.
6. 21cm നീളമുള്ള ഒരു വര വരയ്ക്കുക. 21 cm2 പരപ്പളവുള്ള സമചതുരം വരയ്ക്കുക.

3. സാധ്യതകളുടെ ഗണിതം

1. ഒരു സംഭവത്തിന്‍റെ സാധ്യത

2. അനുകൂല സാധ്യത + പ്രതികൂല സാധ്യത = 1

ചോദ്യങ്ങൾ

1. 52 ചീട്ടുകളുള്ള ഒരു പായ്ക്കറ്റിൽ പകുതി ചീട്ടുകൾ ചുവന്ന നിറമുള്ളവയും ബാക്കി കറുത്ത നിറമുള്ളവയുമാണ്. Hearts, Spade, Clubs, Diamond അടയാളങ്ങളുള്ള 13 ചീട്ടുകൾ വീതമാണ് ആകെയുള്ളത്.
a) അത് കറുത്തതാകാനുള്ള സാധ്യത എത്ര?
b) അത് Spade ആകാനുള്ള സാധ്യത എത്ര?
c) അത് Spade ഒാ Diamond ഒാ ആകാനുള്ള സാധ്യത എത്ര?
a) ആകെ ചീട്ടുകളുടെ എണ്ണം = 52
കറുത്ത ചീട്ടുകളുടെ എണ്ണം = 26
എടുത്ത ചീട്ട് കറുത്തതാകാനുള്ള സാധ്യത

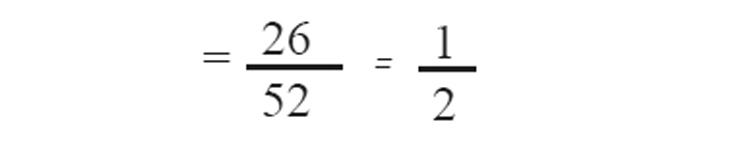
b) Spade ചീട്ടുകളുടെ എണ്ണം = 13
എടുത്ത ചീട്ട് spade ആകാനുള്ള സാധ്യത =

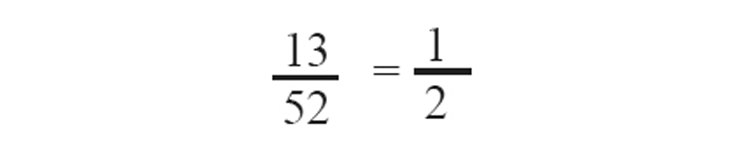
c) Spade ഓ Diamond ഒാ ആയ ചീട്ടുകളുടെ എണ്ണം = 13 +13 =26
എടുത്ത ചീട്ട് Spade ഓ Diamond ഒാ ആകാനുള്ള സാധ്യത =

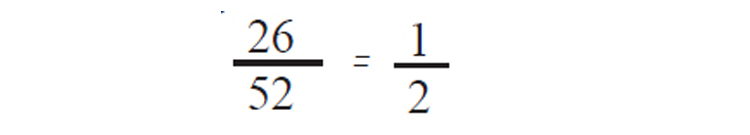
2. ഒരു സമചതുരക്കട്ടയുടെ ഒരു വശത്ത് ഒരു കുത്ത്,മറ്റൊരു വശത്ത് രണ്ട് കുത്ത്,മറ്റൊരു വശത്ത് മൂന്ന് കുത്ത് എന്ന ക്രമത്തിൽ ആറ് വശങ്ങളിലും കുത്തുകൾ ഇട്ടിരിക്കുന്ന ഇതേ പോലുള്ള മറ്റൊരു സമചതുരക്കട്ടകൂടി എടുക്കുന്നു.
a) ഈ രണ്ട് കട്ടകളും ഒരേ സമയം എറിഞ്ഞാൽ മുകൾ വശത്ത് വരുന്ന കുത്തുകളുടെ ആകെ
എണ്ണം 6 വരാനുള്ള സാധ്യത എത്ര?
b) ആകെ കുത്തുകളുടെ എണ്ണം 9 വരാനുള്ള സാധ്യത എത്ര‍?
c) ആകെ കുത്തുകളുടെ എണ്ണം ഒരു അഭാജ്യസംഖ്യ ആകുവാനുള്ള സാധ്യത എത്ര?
ആകെ ജോഡികളുടെ എണ്ണം 36
a) കുത്തുകളുടെ ആകെ എണ്ണം 6 വരുന്ന ജോഡികൾ (1,5) (2,4) (3,3) (4,2) (5,1)
സാധ്യത

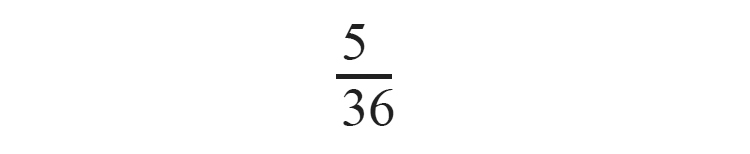
c) 9 വരുന്ന ജോഡികൾ (3,6) (4,5) (5,4) (6,3)
സാധ്യത

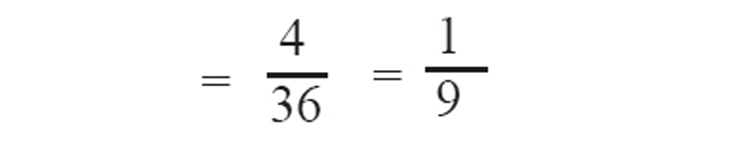
c) 1 വരാനുള്ള സാധ്യത =

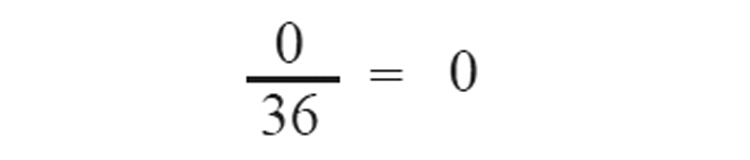
ആകെ കുത്തുകൾ അഭാജ്യസംഖ്യകൾ ആകുന്ന ജോഡികൾ(1,1) (1,2) (1,4) (1,6) (2,1) (2,3) (2,5) (3,2) (3,4) (4,1) (4,3) (5,2),(5,6) (6,1) (6,5)
സാധ്യത

4. രണ്ടാംകൃതി സമവാക്യങ്ങൾ

ഒരു രണ്ടാംകൃതി സമവാക്യത്തിന്‍റെ, സാമാന്യരൂപം ax2+bx+c=0, a=0 ax2+bx+c=0 എന്ന സമവാക്യത്തിൽ "x’ന് പരമാവധി 2 വിലകൾ ഉണ്ട്. x2+ax നെ വർഗം തികയ്ക്കാൻ കൂട്ടിയാൽ മതി.
ax2+bx+c =0 എന്ന സമവാക്യത്തിൽ

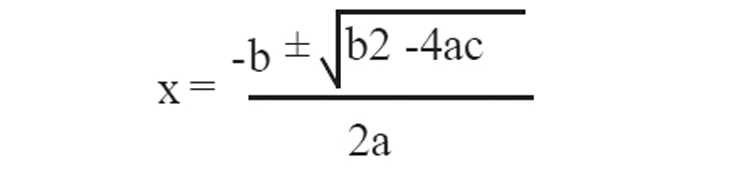
1. ഒരു സംഖ്യയുടെയും അതിന്‍റെ വ്യൂൽക്രമത്തിന്‍റെയും വ്യത്യാസം ഏത് അധിസംഖ്യയുമാകാമെന്ന് സമർഥിക്കുക.
സംഖ്യ = X
വ്യൂൽക്രമം =

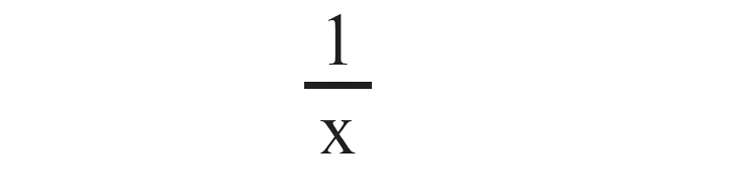
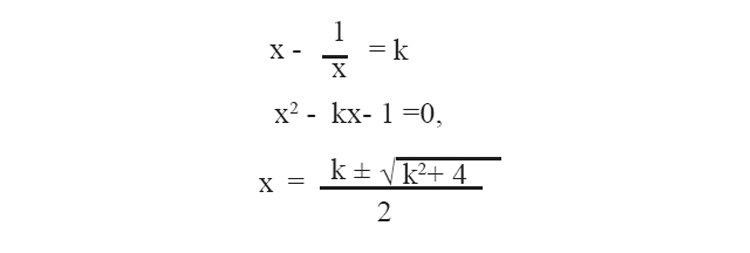
k ഏത് സംഖ്യ ആയാലും k2+4 അധിസംഖ്യയായിരിക്കും.
2. 44 സെ.മീ ചുറ്റളവുള്ള ഒരു ചതുരത്തിന്‍റെ പരപ്പളവ് 117 ച.സെ.മീ ആണ്.
a) സമചതുരത്തിന്‍റെ നീളം 11 സെ.മീ ആയാൽ വീതി എത്ര?
b)ചതുരത്തിന്‍റെ നീളവും വീതിയും കണക്കാക്കുക.
നീളം = 11 + x
വീതി = 22 -(11+ x)
= 11 -x
പരപ്പളവ് (11+ x) (11+ x) = 177
121 x2 =117
x2 = 4
x= 2
നീളം സെമീ = 11 +2 =13 സെ.മീ
വീതി സെമീ = 11- 2 = 9 സെ.മീ
3. രണ്ട് സമചതുരങ്ങളുടെ പരപ്പളവുകളുടെ തുക 500m2 ആണ്.അവയുടെ ചുറ്റളവുകൾ തമ്മിലുള്ള വ്യത്യാസം 40m ആയാൽ സമചതുരത്തിന്‍റെ രണ്ടുവശ ങ്ങൾ കാണുക.
x,y എന്നിവ സമചതുരത്തിന്‍റെ വശങ്ങളായാൽ

x2+y2 = 500
4x-4y =40
x-y = 10
y=x-10
x2 + (x+10)2 = 500
2x2-20x-400=0
x2-10x-200=0
x=20 or x=-10
x,y എന്നിവ സമചതുരത്തിന്‍റെ വശങ്ങളായാൽ വശം നെഗറ്റീവ് ആകില്ല.
x= 20
ഒന്നാമത്തെ സമചതുരത്തിന്‍റെ വശം x= 20m
രണ്ടാമത്തെ സമചതുരത്തിന്‍റെ വശം y= 20-10 = 10m

ത്രികോണമിതി

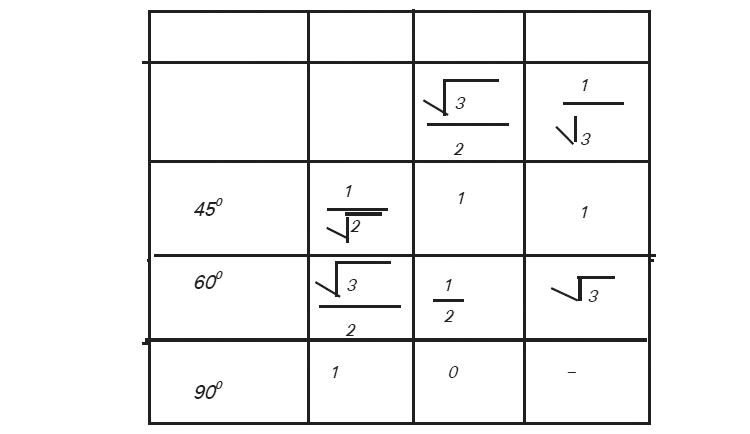
1. ഒരു ത്രികോണത്തിലെ കോണുകൾ അതിലെ വശങ്ങളുടെ അംശബന്ധം നിശ്ചയിക്കുന്നു.
2. കോണുകൾ 450,450,900 ആയ ഏതു ത്രികോണത്തിന്‍റെയും വശങ്ങൾ 1:1: 2 എന്ന അംശബന്ധത്തിലാണ്.
3.കോണുകൾ 300,600,900 ആയ ഏതു ത്രികോണത്തിന്‍റെയും വശങ്ങൾ 1: 3:2 എന്ന അംശബന്ധത്തിലാണ്.
4. ത്രികോണംABC യുടെ രണ്ടുവശങ്ങൾ a,c എന്നിവയും ഇടയിലുള്ളകോണ്‍ B യുമായാൽ , B 900 യിൽ കുറവ് പരപ്പളവ് =

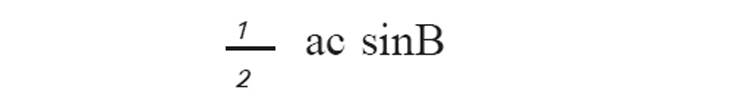
5. ത്രികോണം ABCയുടെ വശങ്ങൾ a,c എന്നിവയും ഇടയിലുള്ള കോണ്‍ Bയും (B,900യ്ക്ക് മുകളിൽ) ആയാൽ പരപ്പളവ് =

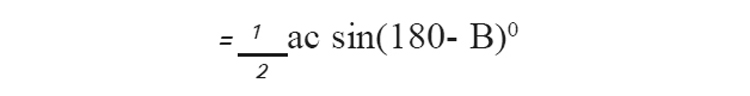
6. കേന്ദ്രകോണ്‍ 600 ആയ ഞാണിന്‍റെ നീളം = ആരത്തിന്‍റെ നീളം
7.കേന്ദ്രകോണ്‍ 1200 ആയ ഞാണിന്‍റെ നീളം= 3 x ആരം
8. "r' ആരമായവൃത്തത്തിലെ ‘c' കേന്ദ്രകോണുകൂടിയ ഞാണിന്‍റെ നീളം =

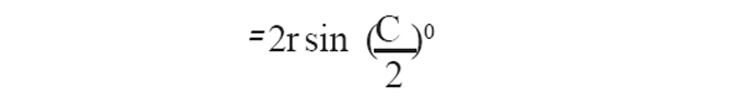
9. മേൽകോണ്‍ (Angle of elevation) : സാധാരണയായി നമ്മുടെ നോട്ടത്തിന്‍റെ പാത നിലത്തിനു സമാന്തരമാണ്. ഉയരത്തിലുള്ളവയെ നോക്കുന്പോൾ ഇത് മേൽപ്പോട്ടുയരും. ഈ രണ്ടു വരകൾ തമ്മിലുള്ള കോണിനെ മേൽകോണ്‍ ((Angle of elevation) എന്നാണ് പറയുന്നത്.
10. കീഴ്കോണ്‍((Angle of depression) : ഉയരത്തിൽ നിൽക്കുന്പോൾ താഴെയുള്ളവയെ കാണാൻ ദൃഷ്ടി താഴ്ത്തേണ്ടി വരുന്പോൾ സാധാരണ നോട്ടത്തിന്‍റെ പാതയും താഴേക്കുള്ള നോട്ടത്തിന്‍റെ പാതയും ഉണ്ടാകുന്ന കോണിനെ കീഴ്കോണ്‍ ((Angle of depression) എന്നാണ് പറയുന്നത്.

ചോദ്യങ്ങൾ

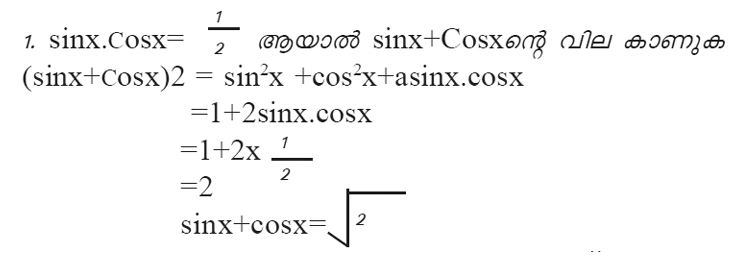
2. അനുവും വിനുവും പട്ടം പറപ്പിക്കുകയാണ്.രണ്ടുപേരുടെയും പട്ടത്തിന്‍റെ നൂലിന്‍റെ 55 മീറ്റർ.രണ്ടുപേരും പരമാവധി നൂലുപയോഗിച്ച സന്ദർഭത്തിൽ അനുവിന്‍റെ നൂലിന്‍റെ അഗ്രം തറയുമായി ഉണ്ടാകുന്ന കോണ്‍ 400യും വിനുവിന്‍റേത് 300 ആണെങ്കിൽ
1.അനുവിന്‍റെയും വിനുവിന്‍റെയും പട്ടങ്ങൾക്ക് തറയിൽ നിന്നുള്ള ഉയരം കണ്ടുപിടിക്കുക.
2. ആരുടെ പട്ടമാണ് തറയിൽ നിന്നും കൂടുതൽ ഉയരത്തിൽ പറക്കുന്നത്? എത്ര കൂടുതൽ

ഉത്തരം

1. അനുവിന്‍റെ പട്ടത്തിന് തറയിൽ നിന്നുള്ള ഉയരം = BD
ത്രികോണ BD യിൽ നിന്നും

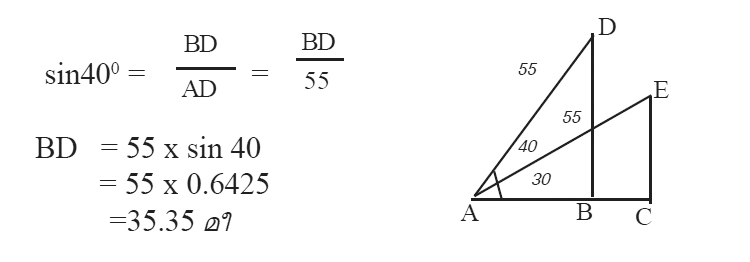
വിനുവിന്‍റെ പട്ടത്തിന് തറയിൽ നിന്നുള്ള ഉയരം
= CE
ACE യിൽ നിന്നും

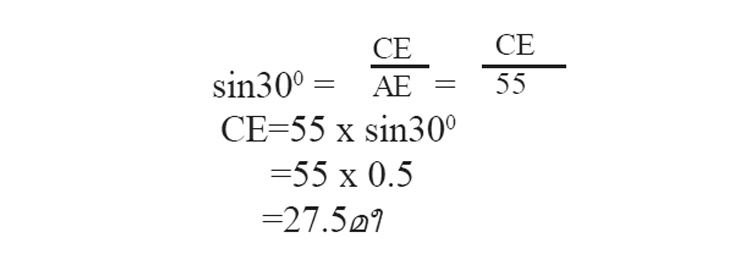
അനുവിന്‍റെ പട്ടമാണ് തറയിൽ നിന്നും കൂടുതൽ ഉയരത്തിൽ പറക്കുന്നത്.
കൂടുതലുള്ള ഉയരം = 35.35 -27.5
= 7.85മീ

5. ഘനരൂപങ്ങൾ

1. ഒരു സമചതുരസ്തൂപികയുടെ മുഖങ്ങളുടെ എണ്ണം 6 ഒരു പാദമുഖവും, 4 പാർശ്വമുഖവും. പാദം സമചതുരവും, പാർശ്വമുഖങ്ങൾ സമപാർശ്വത്രികോണങ്ങളുമാണ്.ആകെ വക്കുകളുടെ എണ്ണം 8,4 പാദവക്കുകളും(b) 4 പാർശ്വവക്കുകളു(c)
2. സ്തൂപികക്ക് രണ്ട് തരം ഉയരങ്ങളുണ്ട്.യഥാർത്ഥ ഉയരം (h), പാർശ്വമുഖങ്ങളുടെ ഉയരമായ ചരിവുയരം (I)

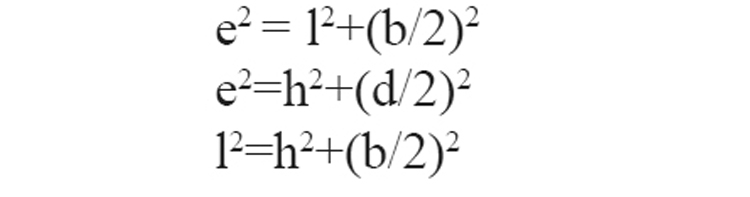
3.സമചതുരസ്തൂപികയുടെ ഉപരിതല വിസ്തീർണ്ണം = b2+2bl
4.സമചതുരസ്തൂപികയുടെ വ്യാപ്തം =

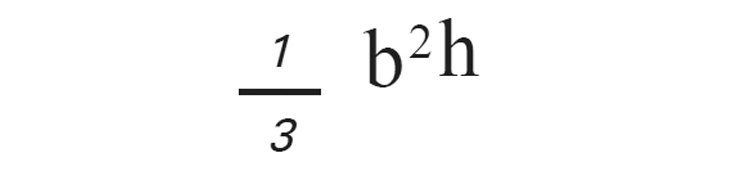
5. വൃത്താംശം മടക്കിയാണ് വൃത്തസ്തൂപിക ഉണ്ടാക്കുന്ന്. R ആരവും X കേന്ദ്രകോണും ഉള്ള വൃത്താംശം മടക്കി ഉണ്ടാകുന്ന വൃത്തസ്തൂപികയുടെ ചരിവുയരം I = R ആണ്. ആരം കാണുവാനുള്ള വാക്യം

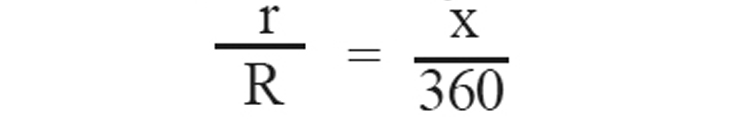
6. വൃത്തസ്തൂപികയുടെ ആരം,ഉയരം,ചരിവുയരം എന്നിവ ബന്ധപ്പെടുത്തുന്ന വാക്യം l2= r2+h2
7.വൃത്തസ്തൂപികയുടെ ഉപരിതലപരപ്പളവ്

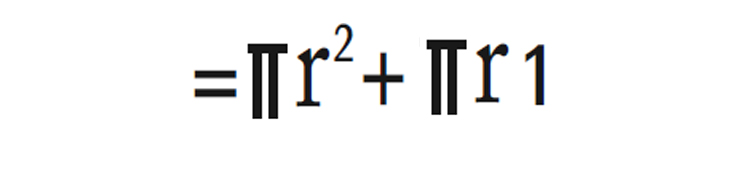
8.വൃത്തസ്തൂപികയുടെ വ്യാപ്തം

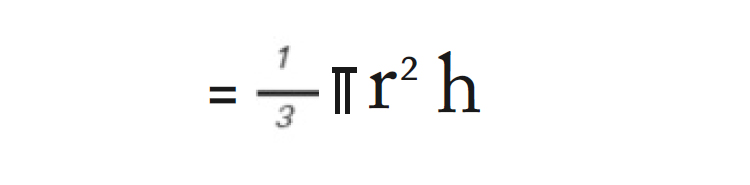
9.ഗോളത്തിന്‍റെ ഉപരിതല വിസ്തീർണ്ണം =
10. ഗോളത്തിന്‍റെ വ്യാപ്തം

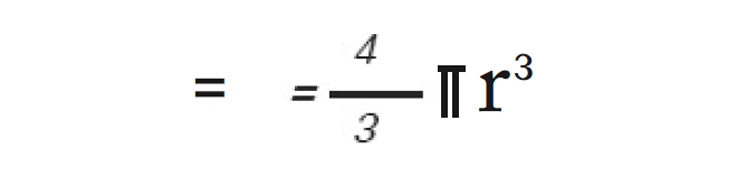
11. അർദ്ധഗോളത്തിന്‍റെ ഉപരിതല വിസ്തീർണ്ണം

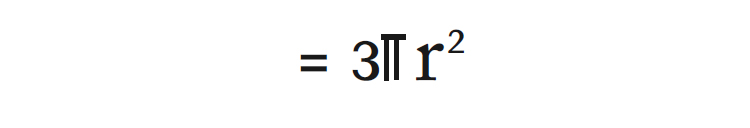
12.അർദ്ധഗോളത്തിന്‍റെ വ്യാപ്തം

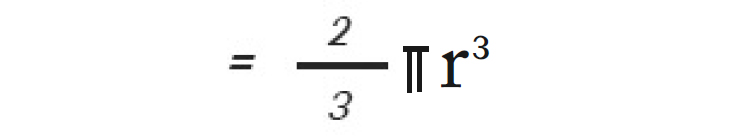
ചോദ്യങ്ങൾ

1. 9 സെന്‍റിമീറ്റർ ആരമുള്ള വൃത്തസ്തൂപികാകൃതിയായ ഒരു പാത്രം ഉപയോഗിച്ച് 12.സെ.മീ ആരവും 15 സെ.മീ ഉയരവുമുള്ള വൃത്തസ്തംഭകൃതിയായ ഒരു പാത്രത്തിൽ പാൽ അളന്നോഴിച്ചു.4 പ്രാവശ്യം ഒഴിച്ചപ്പോൾ പാത്രം നിറഞ്ഞുവെങ്കിൽ വൃത്തസ്തൂപികാകൃതിയായ പാത്രത്തിന്‍റെ ഉയരമെത്ര?
വൃത്തസ്തംഭത്തിന്‍റെ വ്യാപ്തം

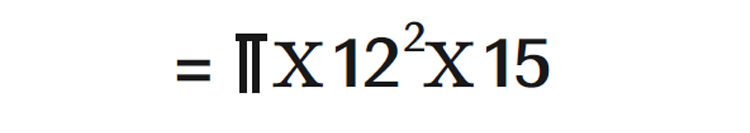
വൃത്തസ്തൂപികയുടെ ഉയരം h ആയാൽ വ്യാപ്തം

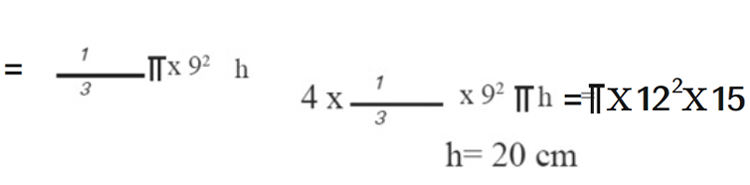
2.മരത്തടിയിൽ നിർമ്മിച്ച ഒരു വൃത്തസ്തൂപികയുടെ പാദ ആരം 30സെ.മീ,ഉയരം 40 സെ.മീ.അതിന്‍റെ ചരിവുയരമെത്ര? ഇത്തരം 10 വൃത്തസ്തൂപികരളുടെ മുഖങ്ങൾ ചായം തേക്കുന്നതിന് ചതുരമീറ്ററിന് 50 രൂപ നിരക്കിൽ ആകെ എത്ര രൂപയാകും.
ചരിവുയരം = 50സെ.മീ
പാദപരപ്പളവ് = 900 ച സെമീ
വക്രതലപരപ്പളവ് = 1500 ചസെ.മീ
10 സ്തൂപികകളുടെ പരപ്പളവ് = 2400 x 10 ച.സെ.മീ
=7.536 ച മീ
ചിലവ് =376.80 രൂപ

9. ജ്യാമിതിയും ബീജഗണിതവും

അംശബന്ധം

ഒരു വരയെ ഒരു ബിന്ദു നിശ്ചിത അംശബന്ധത്തിൽ ഭാഗിക്കുന്ന സാഹചര്യമാണ് ഇവിടെ വിലയിരുത്തപ്പെടുന്നത്.

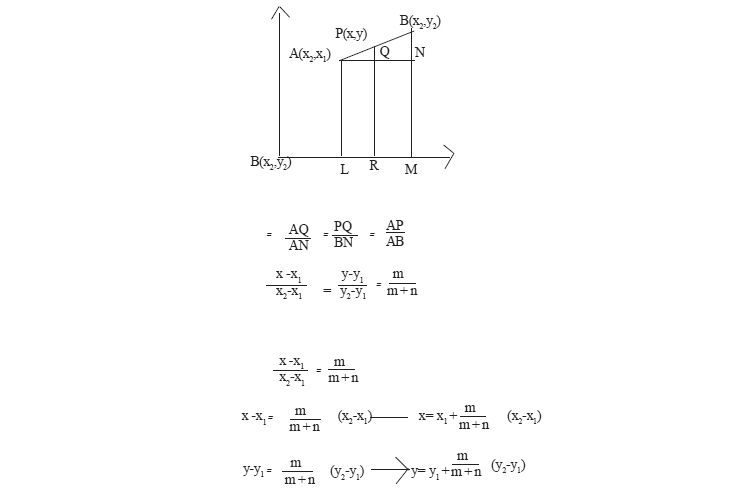
A(x1,y1) B(x2,y2)) എന്നീ ബിന്ദുക്കളെ യോജിപ്പിക്കുന്ന വരയിലെ ബിന്ദുവാണ് P(x,y) PA:PB =m:n ആണ്.അതായത് P(x,y)എന്ന ബിന്ദു A(x1,y1) B(x2,y2) എന്നീ ബിന്ദുക്കൾ യോജിപ്പിക്കുന്ന വരയെ m:n എന്ന അംശബന്ധത്തിൽ ഭാഗിക്കുന്ന Aയുടെയും Bയുടെയും സൂചകസംഖ്യകളുംm,n എന്നീ സംഖ്യകളും ഉപയോഗിച്ച് Pയുടെ സൂചകസംഖ്യകൾ കണ്ടെത്തണം A,P,B എന്നീ ബിന്ദുക്കളിൽ നിന്നും "x' അക്ഷത്തിലേക്ക് ലംബം വരയ്ക്കുക.ചിത്രത്തിൽ ത്രികോണം ANB , ത്രികോണം AQP എന്നീവ സദൃശ്യത്രികോണങ്ങളാണ്.

ചോദ്യം

1. (1,6) 5,2) എന്നീ ബിന്ദുക്കൾ യോജിപ്പിക്കുന്ന വരയെ മൂന്ന് സമഭാഗങ്ങളാക്കുന്ന ബിന്ദുക്കളുടെ സൂചകസംഖ്യകൾ കണക്കാക്കുക.
C, D എന്നീബിന്ദുക്കൾ
ABയെ 3 തുല്യഭാഗങ്ങളാക്കുന്നു.
AC:DB=1:2
AD:DB=2:1
"c’യുടെ x സൂചകസംഖ്യx =

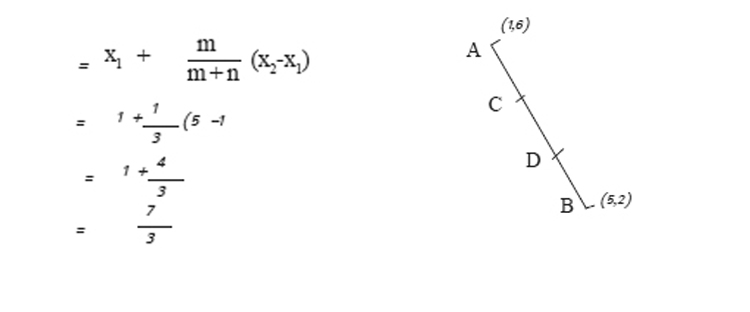
"y' സൂചകങ്ങളുടെ സംഖ്യ y

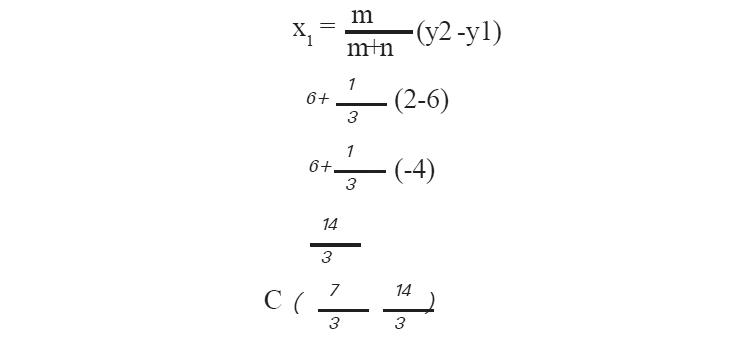
D യുടെ "x' സൂചകസംഖ്യ =

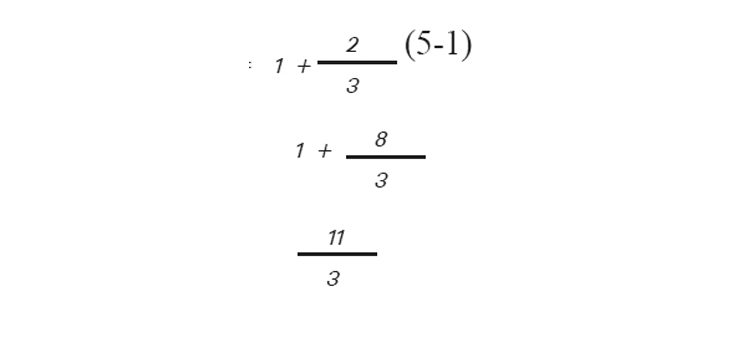
"y' സൂചകസംഖ്യ =

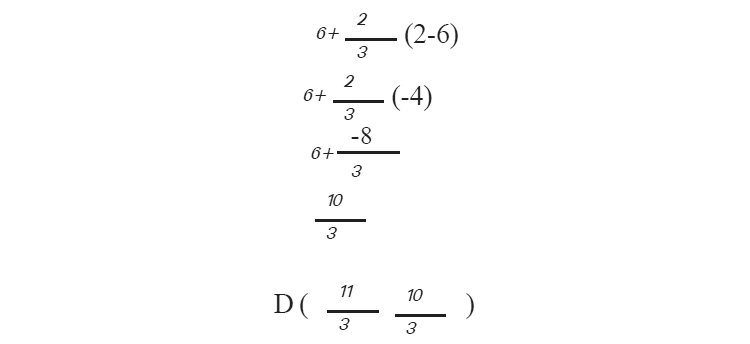
വരക്കണക്ക്
നാലുതരം വരകളുണ്ട്

1. "x ’അക്ഷത്തിന് സമാന്തരമായ വരകൾ
2. "x' അക്ഷത്തിന് സമാന്തരമായ വരകൾ
3. വലത്തേക്ക് ചരിഞ്ഞ വരകൾ
4. ഇടത്തേക്ക് ചരിഞ്ഞ വരകൾ
1. ഒരു വരയ്ക്ക് "x'അക്ഷത്തിന്‍റെ പോസ്റ്റീവ് ദിശയുമായി രൂപീകരിക്കുന്ന കോണിന്‍റെ tan അളവാണ് വരയുടെ ചരിവ്
2. A(x1y1) B(x2y2)എന്നീ ബിന്ദുക്കളിലൂടെ കടന്നു പോകുന്ന വരയുടെ ചരിവ്

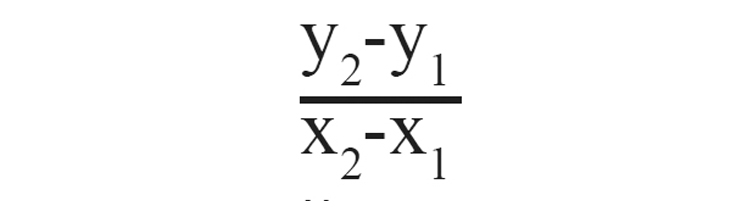
3. ഒരു വരയ്ക്ക് ഒരു ചരിവ് മാത്രമേ ഉണ്ടാകൂ. ചരിവ് കണക്കാക്കുന്നതിന് വരയിലെ ഏതെങ്കിലും രണ്ട് ബിന്ദുക്കൾ പരിഗണിച്ച് ക്രിയ ചെയ്യുക.
4. മൂന്ന് ബിന്ദുക്കൾ ഒരു വരയിലാണോ എന്ന് പരിശോധിക്കുന്നതിന് ചരിവ് എന്ന ആശയം ഉപയോഗിക്കുന്നു.
5. വരകൾ സമാന്തരവരകൾ ആണെങ്കിൽ അവയുടെ ചരിവ് തുല്യമായിരിക്കും.
6.ലംബങ്ങളുടെ ചരിവുകളുടെ ഗുണനഫലം -1 ആണ്.
7. ‘x' സൂചകസംഖ്യകളും"y’ സൂചകസംഖ്യകളും സമാന്തര ശ്രേണിയിലായ ബിന്ദുക്കളെല്ലാം ഒരു വരയിലായിരിക്കും.

രൂപങ്ങളും സമവാക്യങ്ങളും

"x’അക്ഷത്തിലെ ബിന്ദുക്കളുടെ "y’ സൂചകസംഖ്യ പൂജ്യമാണ്. y=0 എന്നത് xഅക്ഷത്തിന്‍റെ സമവാക്യമാണ്.
"y' അക്ഷത്തിലെ ബിന്ദുക്കളുടെ "x’സൂചകസംഖ്യ പൂജ്യമാണ് x=0 എന്നത് ്y അക്ഷത്തിന്‍റെ സമവാക്യമാണ്.
ഏതൊരു വരയ്ക്കും സമവാക്യം ഉണ്ടായിരിക്കും.
ഒരു വരയിലെ ബിന്ദുക്കളുടെ "x’ സൂചകസംഖ്യയും "y’ സൂചകസംഖ്യയും തമ്മിലുള്ള ബന്ധമാണ് വരയുടെ സമവാക്യമായി എഴുതുന്നത.് (1,2),(2,2) (3,3) എന്നീ ബിന്ദുക്കളിലൂടെ കടന്നു പോകുന്ന വരയുടെ സമവാക്യം x=y എന്നതാണ്.
ax+by+c =0 എന്ന വരയുടെ ചരിവ്

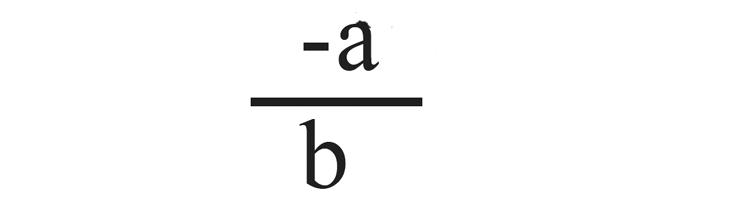
വൃത്തത്തിന്‍റെ സമവാക്യം

1. x2+y2=r2 എന്നത് ആരം "r’ ആയതും (x, y)
ആധാരബിന്ദു കേന്ദ്രമായതും ആയ
വൃത്തത്തിന്‍റെ സമവാക്യമാണ്.
2. കേന്ദ്രം(x1,y1) ആരം "r' വൃത്തിലെ ഒരു ബിന്ദു
(x, y) ആയാൽ വൃത്തത്തിന്‍റെ സമവാക്യം
(x-x1)2 + (y-,y1)2 =r2 ആയിരിക്കും.
3. (x1, y1) (x2, y2) എന്നീ ബിന്ദുക്കൾ
യോജിപ്പിക്കുന്ന വരയിലെ ഒരു ബിന്ദു (x, y)
ആയാൽ ആ വരയുടെ സമവാക്യം

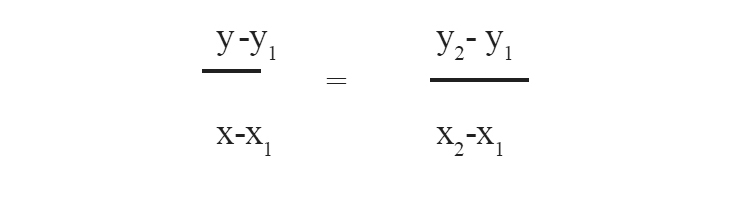
ആണ്.

4. ഒരു സാമാന്തരികത്തിന്‍റെ നാലു മൂലകൾ ക്രമത്തിൽ(x1,y1)(x2,y2)(x3,y3)(x4,y4) ഇവ ആയാൽ x1,+ x3 = x2 +x4 y1+y3 = y2+y4

ബഹുപദങ്ങൾ

1. P(x) എന്ന ബഹുപദത്തിനെ x-a കൊണ്ട് ഹരിച്ചാൽ കിട്ടുന്ന ശിഷ്ടംP(a)
2. . P(x) എന്ന ബഹുപദത്തിനെ x+a കൊണ്ട് ഹരിച്ചാൽ കിട്ടുന്ന ശിഷ്ടം P(-a)
3. . P(x) എന്ന ബഹുപദത്തിന്‍റെ ഘടകമാണ് x-a എങ്കിൽ P(a)=0
4. P(x) എന്ന ബഹുപദത്തിന്‍റെ ഘടകമാണ് x+a എങ്കിൽ P(-a)=0

1. 2x2-3x-1 എന്ന പോളിനോമിയലിനോട് ഏത് സംഖ്യ കൂട്ടിയാൽ x-1 , പോളിനോമിയലിന്‍റെ ഒരു ഘടകമാകും?
P(x) = 2x2-3x-1
P(x)+ k യുടെ ഘടകമാണ് x-1 എന്ന് കരുതുക
P(x)+ k= 2x2-3x-1+k
2x12-3 x 1-1+k=0
p(1)=-2
p(1)k=0 ആയാൽ k=2
P(x) എന്ന ബഹുപദത്തെ x-a കൊണ്ട് ഹരിക്കുന്പോഴുള്ള ശിഷ്ടം k യും Q(x) നെ x-a കൊണ്ട് ഹരിക്കുന്പോഴുള്ള ശിഷ്ടം -k യും ആയാൽ P(x) +Q(x) ന്‍റെ ഘടകമാണ് x-a എന്ന് തെളിയിക്കുക.
P(x) നെ x-a കൊണ്ട് ഹരിക്കുന്പോഴുള്ള ശിഷ്ടം P(a)=k
P(x) നെ x-a കൊണ്ട് ഹരിക്കുന്പോഴുള്ള ശിഷ്ടംQ(a)=-k
P(x) +Q(x) നെ കൊണ്ട് ഹരിക്കുന്പോഴുള്ള ശിഷ്ടം =P(a)+Q(a)
= k-k
=0
x-a,p(x)+Q(x) ഘടകമാണ്.

സ്ഥിതി വിവരക്കണക്ക്
1. ലോംഗ് ജംപ് പരിശീലനത്തിൽ ഒരാൾ ചാടിയ ദൂരങ്ങൾ ഇങ്ങനെയാണ്. 6.10,6.20 6.18,6.20 6.25,6.21 6.15,6.10 ഇവയുടെ മാധ്യവും മധ്യമവും കണ്ടുപിടിക്കുക.
മധ്യമം കാണാൻ ഇവയെ ആരോഹണക്രമത്തിൽ എഴുതി മധ്യത്തിലേത് എടുക്കുക.

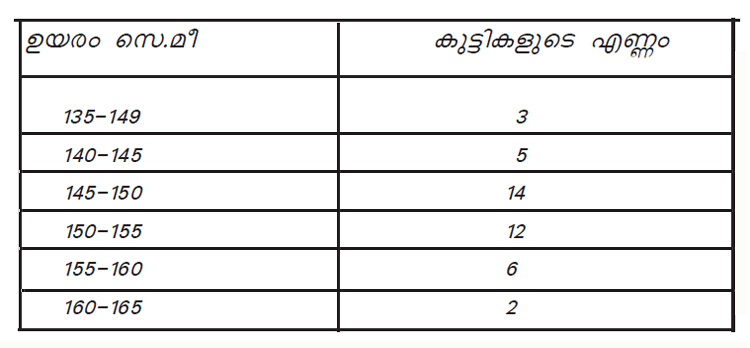
2. ഒരു സ്കൂളിലെ 10-ാം ക്ലാസ്സിൽ പഠിക്കുന്ന കുട്ടികളുടെ ഉയരം എണ്ണം തിരിച്ച് പട്ടികയായി ചുവടെ കൊടുത്തിരിക്കുന്നു.മാധ്യമ ഉയരം കണ്ടുപിടിക്കുക.

മെർലിൻ ഫിലിപ്പ്
സെന്‍റ് ജോർജ് എച്ച്എസ്എസ്, മണിമല

Deepika.com shall remain free of responsibility for what is commented below. However, we kindly request you to avoid defaming words against any religion, institutions or persons in any manner.